Lima, junio de 2024, 8(1), pp. 246-261
Sobre Matrices y Polirritmias
About Matrices and Polyrhythms
Josué Alexis Lugos Abarca↓
Centro Universitario de Música Fermatta
Acapulco de Juárez, México
![]() https://orcid.org/0000-0001-8980-7748
https://orcid.org/0000-0001-8980-7748
DOI
Resumen
El presente artículo busca proponer un método de composición de polirritmias mediante el uso de las matemáticas. Para ello, se emplea la notación box y los patrones de duración para construir un patrón rítmico con un pulso acentuado. Este pulso, denominado “pulso eje”, se desplaza a lo largo de cada posición de la notación durational pattern, lo que permite obtener diferentes patrones rítmicos. Estos patrones se agrupan en una matriz, representando así una polirritmia. Por último, se propone la suma y resta de matrices como un recurso creativo para generar más polirritmias.
Palabras clave
Composición; polirritmia; matrices; suma y resta de matrices; Durational patterns
Abstract
The present article seeks to propose a method of composing polyrhythms through the use of mathematics. For this purpose, box notation and duration patterns are used to construct a rhythmic pattern with an accentuated pulse. This accented pulse, called the “axis pulse”, is shifted along each position of the durational pattern notation, allowing different rhythmic patterns to be obtained. These patterns are grouped in a matrix, thus representing a polyrhythm. Subsequently, addition and subtraction of matrices is proposed as a creative resource to generate more polyrhythms.
Keywords
Composition; Polyrhythmicity; Matrices; Matrix Addition and Subtraction; Durational Patterns
Recibido: 15 de marzo de 2023 / Aceptado: 18 de abril de 2023
Introducción
El uso de las matemáticas en la música como recurso creativo no es nuevo. Varios sistemas armónicos se basan o se inspiran en procesos de índole matemática. Por mencionar algunos, se tiene la teoría del conjunto de clases de altura (Chapman, 1981; Forte, 1974; Vázquez, 2006), la teoría neo-riemanniana (Cannas, 2018; Gollin & Rehding, 2014), las teorías geométricas de los acordes de Tymoczko (2006; 2011), los ejes axiales de Bartok (Lendvai, 2017), los cambios de Coltrane (Porter et al., 2013), entre otros.
Como es notable, tales métodos de composición se centran en las melodías y acordes, siendo este último parámetro el más destacado en el área de investigación. Por otro lado, en cuanto al ritmo, resalta la teoría geométrica del ritmo de Toussaint (Gómez-Martín, 2022; Toussaint, 2019) y los ritmos euclidianos (Toussaint, 2005); un algoritmo enfocado en generar distintos ritmos (Morrill, 2023), los cuales han sido de mucha utilidad en la práctica musical (Rentsch, s.f.).
Asociado al ritmo se encuentra una técnica llamada polirritmia, que estudia todos aquellos patrones rítmicos que se ejecutan simultáneamente (Vallejo, 1995; Randel, 2003), y cuya base se asocia con el contrapunto. De hecho, un simple patrón rítmico puede considerarse polirritmia, como la clave de son, cuya interpretación requiere diferentes medidas métricas (Novotney, 1998).
La polirritmia tiene una gran importancia en la música, ya que su uso se extiende a todos los géneros, ya sea popular, clásica, contemporánea, africana, etc. (Arandia Riveros, 2012). Si bien la teoría geométrica del ritmo analiza la polirritmia, no hace mucho esfuerzo en ofrecer métodos de composición más allá de un método de análisis. Por ende, en este artículo se propone un método matemático de composición para crear polirritmias a partir de los fundamentos de la teoría de Toussaint (2005). Se usará el concepto de las matrices y su álgebra como recurso creativo.
1. Construyendo Matrices Polirritmias
En 1962, Philip Harland desarrolló la notación box, un método de escritura para representar los pulsos de un patrón rítmico, también conocido como “Time Unit Box System” (Toussaint, 2002; Toussaint, 2004; Teitelbaum & Toussaint, 2006). Este se puede representar de la siguiente manera (Toussaint, 2019):
Figura 1
Clave de son

Que musicalmente representa la clave de son.

Nota. Elaboración propia.
Este método permite expresar cualquier patrón rítmico según la acentuación del pulso y sus silencios, los cuales se escriben con “x” y “∙” respectivamente. Otra manera de expresar los patrones rítmicos es mediante los durational patterns, una notación que resume la notación box enumerando a partir de cada pulso (Breslauer, 1988).
Por ejemplo, el durational pattern de 1.1 es:

Es mediante esta notación que se construyen las matrices de polirritmias. Para ilustrar, considérese el siguiente patrón rítmico:

Cuya traducción rítmica es:
Figura 2
Patrón rítmico 1.3.

Nota. Elaboración propia.
Como se explicó, la notación durational pattern sólo indica el pulso que cada figura rítmica genera; no obstante, se puede complementar esta notación indicando una acentuación (Vaissière, 1991; Monahan & Carterette, 1985). Se representará esta articulación (Herrera, 2022) usando el símbolo: ̂ por encima del pulso.
A continuación, en 1.3 se coloca la acentuación aquí:

Cuya traducción rítmica es:
Figura 3
Patrón rítmico 1.3. con acentuación

Nota. Elaboración propia.
A cada pulso que tenga una acentuación se llamará “pulso eje”. El concepto del pulso eje es fundamental en las matrices de polirritmias, ya que será la guía para realizar una clase de permutación (Balakrishnan, 2000) con ciertas condiciones. Se busca que el pulso eje se encuentre en las tres posiciones de 1.4; es decir, se debe recorrer el pulso eje de esta manera:

Como se observa en 1.5, el pulso eje está presente en las tres posiciones de la notación durational patterns, el cual contiene la acentuación. Esta disposición de números da la oportunidad de agruparlas en una matriz (Schneider & Barker, 1989). Por lo tanto, se escribe:

Musicalmente, la matriz 1.6 se puede interpretar como una polirritmia (Vallejo, 1995), ya que la forma de la matriz hace entender que los patrones rítmicos se interpretan simultáneamente. Por lo tanto,
Figura 4
Polirritmia de la matriz 1.6.

Nota. Elaboración propia.
En esta representación, los instrumentos son bongós, congas y claves, de arriba hacia abajo, respectivamente.
Se colocará un número en la parte superior derecha de la matriz con el propósito de indicar el número de compases que la polirritmia se repetirá. Es decir:

Mientras tanto, las barras de repetición se señalarán con las letras “BR” en la parte inferior derecha.

Y el quebrado rítmico estará en la parte superior izquierda de la matriz:

El tempo y la dinámica de cada figura rítmica no serán necesarias indicarse en la matriz. Por ejemplo: si se añaden los siguientes parámetros a la matriz 1.6.

En la partitura, esto se indica de la siguiente manera:
Figura 5
Polirritmia de la matriz 1.10.

Nota. Elaboración propia.
Considérese el siguiente patrón rítmico en su notación durational pattern.

Se coloca la acentuación.

Se recorre el pulso eje de modo que se encuentre en las tres posiciones.

Por último, se agrupan en una matriz. Se definen cuántos compases se va a repetir el patrón, si tendrá barra de repetición y su respectivo quebrado rítmico.

De esa manera, se obtiene la siguiente polirritmia:
Figura 6
Polirritmia de la matriz 1.14

Nota. Elaboración propia.
2. Operaciones de matrices para componer más polirritmias
En la sección anterior, se logró expresar polirritmias mediante matrices. Matemáticamente, las matrices tienen la capacidad de ser operadas entre sí mediante suma, resta, multiplicación y división (Friedland, 2015). Se aprovechará esta herramienta matemática como un recurso creativo, ya que a través de tales operaciones surge un método para crear nuevas polirritmias.
Por ejemplo, tómese de referencia las matrices 1.10 y 1.14, y súmense de la siguiente manera:

Es fácil de observar que el resultado es otra matriz, la cual puede representar una polirritmia. Se reescribe la matriz resultante asignando los compases que se repetirá el patrón, la barra de repetición, el quebrado rítmico y la acentuación.

Lo que en la partitura se indica como:
Figura 7
Polirritmia de la matriz 2.2
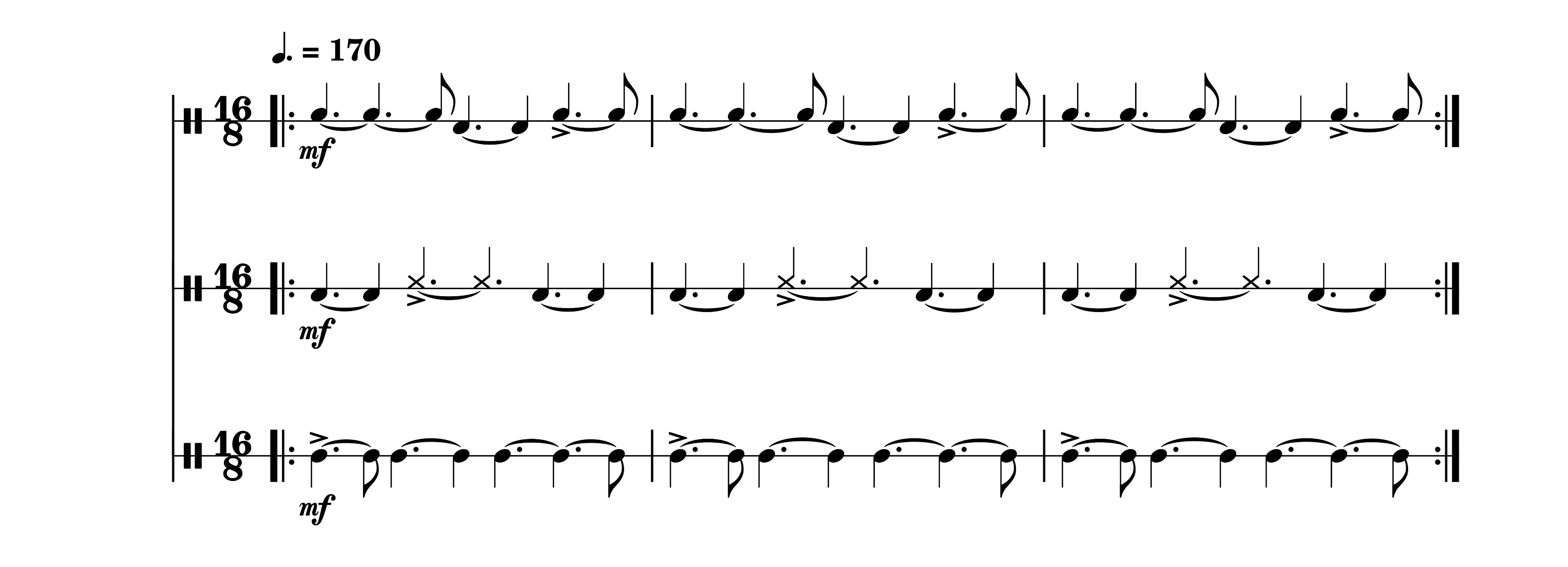
Nota. Elaboración propia.
A las matrices polirrítmicas que surjan de cualquier operación se llamarán matrices polirrítmicas compuestas. Debido a que, al realizar una suma o cualquier operación, no se tiene el control sobre los números resultantes, para esta clase de matrices, el concepto del pulso eje no se aplica, tal como se observa en la matriz 2.2.
Tómese nuevamente las matrices 1.10 y 1.14, pero en lugar de sumarlas, ahora réstense:

Se interpretará cualquier número negativo y cero como un silencio. Por lo tanto:

Figura 8
Polirritmia de la matriz 2.4

Nota. Elaboración propia.
Como compositor, se pueden tomar las matrices 1.10, 1.14, 2.2 y 2.4, y colocarse en una sola secuencia. De esta manera, se componen cuatro compases, es decir:
Figura 9
Polirritmia de la matriz 2.2

Nota. Elaboración propia.
Conclusiones
En este artículo se propuso un método matemático para componer polirritmias mediante el uso de matrices y su álgebra. Debido a su proceso, este método permite obtener diversas polirritmias interesantes, ya que el compositor tiene total libertad en cuanto a los parámetros musicales y los acentos que se utilizarán. Es decir, a pesar de ser un método matemático, su metodología permite involucrar un gran proceso creativo al emplearlo. Dicho proceso de composición se diseñó de manera flexible y sin generar limitantes hacia cualquier tipo de creatividad.
Además, las operaciones de matrices (suma, resta, multiplicación y división) amplían aún más el alcance creativo. Por ejemplo, permiten crear cadenas de polirritmias que se pueden aplicar a secciones de percusión, a secciones melódicas como un cuarteto de cuerdas e incluso a percusiones modernas denominadas “beats”.
Referencias
Arandia Riveros, M. A. (2012). Clasificación del uso de métricas irregulares, polirritmias, desplazamientos y modulaciones métricas a partir del análisis e interpretación de cinco temas de jazz y rock [Tesis de maestría, Universidad Distrital Francisco José de Caldas]. RIUD Principal. http://hdl.handle.net/11349/1130
Balakrishnan, V. K. (2000). Introductory discrete mathematics. Dover Publications.
Breslauer, P. (1988). Diminutional rhythm and melodic structure. Journal of Music Theory, 32(1), 1-21.
Cannas, S. (2018). Geometric representation and algebraic formalization of musical structures. [Tesis doctoral, Université de Strasbourg; Università degli studi di Pavia]. Portail HAL Theses. https://theses.hal.science/tel-02179522
Chapman, A. (1981). Some intervallic aspects of pitch-class set relations. Journal of Music Theory, 25(2), 275-290. https://doi.org/10.2307/843652
Forte, A. (1974). Structure of Atonal Music. Yale University Press.
Friedland, S. (2015). Matrices: Algebra, Analysis And Applications. World Scientific Publishing.
Gollin, E., & Rehding, A. (Eds.). (2014). The oxford handbook of Neo-Riemannian music theories. Oxford University Press.
Gómez-Martín, F. (2022). A review of Godfried Toussaint's The Geometry of Musical Rhythm. Journal of Mathematics and Music, 16(2), 239-247.
Herrera, E. (2022). Teoría Musical y Armonía Moderna vol. 1. Antoni Bosch Editor.
Lendvai, E. (2017). Bela Bartók. Un análisis de su música [Material Complementario]. http://sedici.unlp.edu.ar/handle/10915/73505
Monahan, C. B., & Carterette, E. C. (1985). Pitch and duration as determinants of musical space. Music Perception, 3(1), 1-32.
Morrill, T. (2023). On The Euclidean Algorithm: Rhythm Without Recursion. Bulletin of the Australian Mathematical Society, 107(3), 361-367.
Novotney, E. D. (1998). The 3: 2 relationship as the foundation of timelines in West African musics [Doctoral dissertation, University of Illinois at Urbana-Champaign].
Porter, L., DeVito, C., Wild, D., Fujioka, Y., & Schmaler, W. (2013). The John Coltrane reference. Routledge.
Randel, D. M. (Ed.). (2003). The Harvard dictionary of music: Fourth edition. Belknap Press.
Rentsch, A. (s.f.). Mathematical Investigations into Rhythm. La Trobe University.
Schneider, H., & Barker, G. P. (1989). Matrices and Linear Algebra. Dover Publications.
Teitelbaum, J., & Toussaint, G. (2006, 4-8 de agosto). RHYTHMOS: An interactive system for exploring rhythm from the mathematical and musical points of view.En R. Sarhangi y J. Sharp (Eds.). Bridges London: Mathematics, Music, Art, Architecture, Culture. Londres.
Toussaint, G. (2002). A mathematical analysis of African, Brazilian, and Cuban clave rhythms. En R. Sarhangi (Ed.). Bridges London: Mathematics, Music, Art, Architecture, Culture. Londres.
Toussaint, G. (2005, 31 de julio - 3 de agosto). The Euclidean algorithm generates traditional musical rhythms. En R. Sarhangi y R. Moody (Eds.). Renaissance Banff: Mathematics, Music, Art, Culture, Alberta.
Toussaint, G. T. (2004, 10-14 de octubre). A Comparison of Rhythmic Similarity Measures. En International Society for Music Information Retrieval Conference - ISMIR, 5th International Conference on Music Information Retrieval Audiovisual Institute, Universitat Pompeu Fabra, Barcelona.
Toussaint, G. T. (2019). The geometry of musical rhythm: What makes a “good” rhythm good?, second edition (2nd ed.). CRC Press.
Tymoczko, D. (2006). The geometry of musical chords. Science, 313(5783), 72–74.
Tymoczko, D. (2011). A geometry of music: Harmony and counterpoint in the extended common practice. Oxford University Press.
Vaissière, J. (1991). Rhythm, accentuation and final lengthening in French. In Music, Language, Speech and Brain: Proceedings of an International Symposium at the Wenner-Gren Center, Stockholm, 5–8 September 1990 (pp. 108-120). Macmillan Education UK.
Vallejo, P. (1995). Del pulso a la polirritmia. Una experiencia creativa. Quodlibet, (2), 35-58.
Vázquez, H. (2006). Fundamentos teóricos de la música atonal. UNAM.